programmers.co.kr/learn/courses/30/lessons/62048
코딩테스트 연습 - 멀쩡한 사각형
가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을
programmers.co.kr
[풀이]
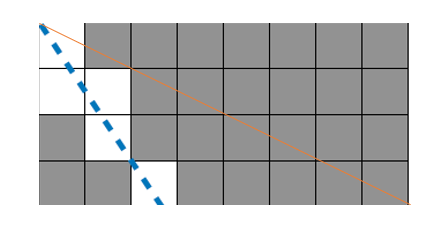
(파란선 무시)
위 w=8, h=4인 사각형에서 빨간 선을 보면 가로선 8개 세로선 4개를 지나오는 모습을 볼 수 있다.
또 다르게 말하면, 꼭짓점에 선이 지나가는 것을 기준으로 가로선 2개, 세로선 1개의 묶음 4개를 볼 수 있다.
이때, 꼭짓점을 지나갔을 경우 가로선과 세로선이 만남으로, 그 선은 하나로 치자. -> 묶음 당 1개를 빼야해
그러면, 총 지나온 선의 수는 (w+h) - 묶음의 갯수 = (8+4) - 4

(파란선 무시)
그렇다면 선이 지나오는 동안 만나는 꼭짓점이 없다면 어떨까?
일단 동일하게 선이 지나온 가로 세로의 갯수를 세어 보자.
가로 선 = 7, 세로 선 = 12
유일하게 만난 꼭짓점은 끝에 한개이므로, 1 묶음이 된다.
그러면 지나온 선은 (7+12) - 1
마지막으로, 저 묶음의 갯수는 어떻게 구할까?
위의 예제에서 보면 첫번째 예제의 경우, 가로 8, 세로 4일 경우 2x1 크기의 묶음 4개가 나왔다.
두번째 예제의 경우, 가로 7, 세로 12일 경우 7x12크기의 묶음 1개가 나왔다.
이로써, 묶음의 갯수는 가로길이와 세로길이의 최대공약수가 됨을 알 수 있다.
따라서, 총 사각형의 갯수 - 선이 지나가는 사각형의 갯수 = (w*h) - (w+h)-(w,h의 최대공약수)
[코드]
from math import gcd
def solution(w,h):
return w*h - ((w+h)-gcd(w,h))'코딩 테스트 > 문제 풀기' 카테고리의 다른 글
| [프로그래머스] 다리를 지나는 트럭 (0) | 2021.03.24 |
|---|---|
| [프로그래머스] 프린터 (0) | 2021.03.24 |
| [프로그래머스] 수식 최대화 (0) | 2021.03.23 |
| [프로그래머스] 짝지어 제거하기 (0) | 2021.03.23 |
| [프로그래머스] N개의 최소공배수 (0) | 2021.03.23 |
댓글